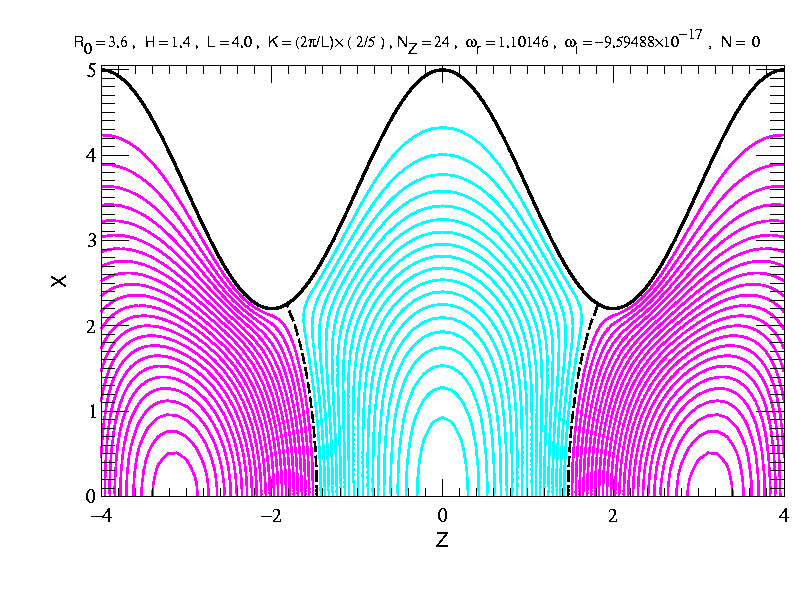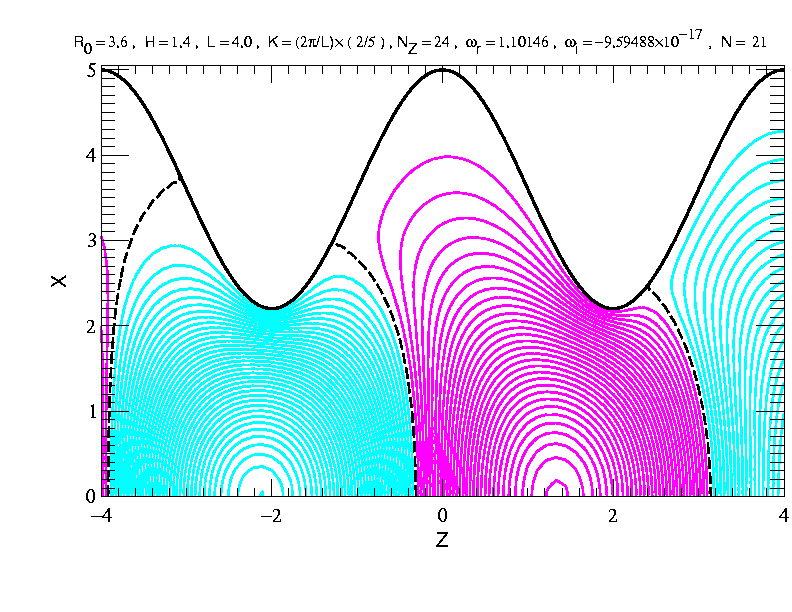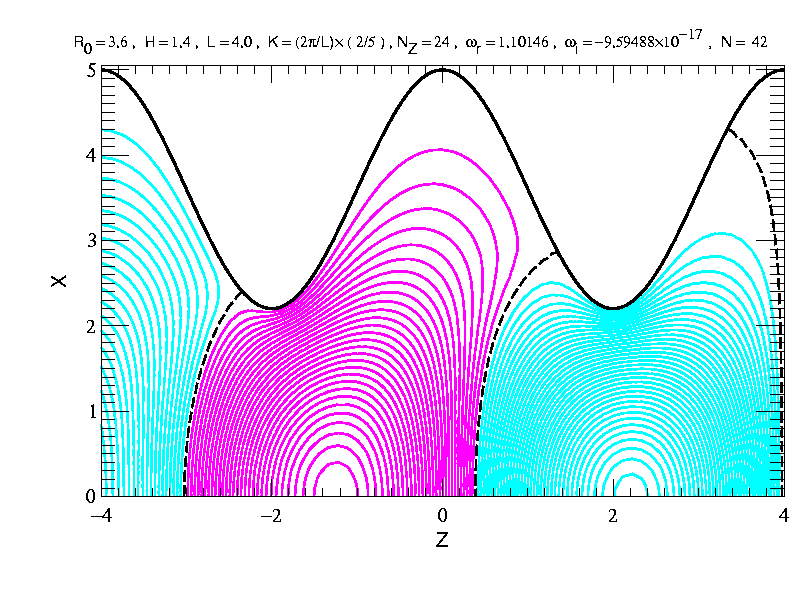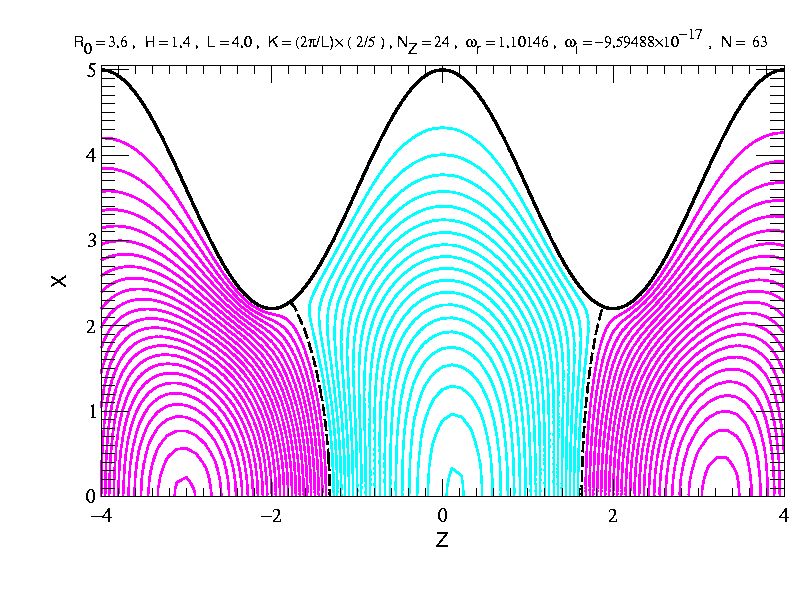
この電界計算の導出を下記に述べる。
1. 位相因子
空間を隔てて伝わる電気信号、すなわち平面波である電磁波の電場ベクトル$\boldsymbol{E}(\boldsymbol{r},t)$は、 伝搬強度ベクトル$\boldsymbol{E}_0$、周波数$\omega$、波数ベクトル$\boldsymbol{k}=(k_z,k_y,k_z)$、座標$\boldsymbol{r}=(x,y,z)$から、 \begin{eqnarray} \boldsymbol{E}(\boldsymbol{r},t)=\boldsymbol{E}_0 \exp \left\{ i (\omega t-\boldsymbol{k} \cdot \boldsymbol{r}) \right\} \label{eq:WavePhaseEq} \end{eqnarray} で定義される。指数部を位相因子と呼ぶ。通常、電場強度を求める複素共益の積により、指数部分は消去される。2.波動関数の導出
Maxwell方程式は次の4式からなる。\begin{eqnarray} \nabla \cdot {\boldsymbol{E}} &=& \cfrac{\rho}{\epsilon_0} \quad\quad\quad\quad\quad\quad\text{Gaussの式} \label{eq:divE}\\ \nabla \times {\boldsymbol{E}} &=& -\cfrac{\partial \boldsymbol{B}}{\partial t} \quad\quad\quad\quad\quad \text{Faradayの式} \label{eq:rotE}\\ \nabla \cdot {\boldsymbol{B}} &=& 0 \quad\quad\quad\quad\quad\quad\quad\quad \text{磁束保存の式} \label{eq:divB}\\ \nabla \times {\boldsymbol{B}} &=& \mu_0 \boldsymbol{J} + \epsilon_0 \mu_0 \cfrac{\partial \boldsymbol{E}}{\partial t} \quad\quad\quad \text{Ampereの式} \label{eq:rotB} \end{eqnarray}
Faradayの式(\ref{eq:rotE})と$\nabla$の外積をとり、左辺はベクトルの三重積、右辺はMaxwell方程式で展開すると、 \begin{eqnarray} \nabla \times (\nabla \times {\boldsymbol{E}}) &=& -\cfrac{\partial }{\partial t}(\nabla \times \boldsymbol{B}) \nonumber \\ \nabla (\nabla \cdot {\boldsymbol{E}})-\nabla^2 {\boldsymbol{E}}&=& \mu_0 \cfrac{\partial }{\partial t} \boldsymbol{J}+ \epsilon_0 \mu_0 \cfrac{\partial^2 \boldsymbol{E}}{\partial t^2} \nonumber \\ -\nabla^2 {\boldsymbol{E}}&=& \cfrac{1}{c^2} \cfrac{\partial^2 \boldsymbol{E}}{\partial t^2} \label{eq:wrotE} \end{eqnarray} となる。右辺の展開では、真空・磁場無し(電荷無し・電流無し)と仮定し、$\boldsymbol{J}=0$、$\rho=0$を利用している。$\epsilon_0$は真空の誘電率、$\mu_0$は真空の透磁率である。光速$c$に対し、$1/c^2=\epsilon_0 \mu_0$を利用した。
電場の式(\ref{eq:WavePhaseEq})から、$\partial/\partial t =i \omega$及び$\nabla =i k_r$となる。これを、 式(\ref{eq:wrotE})に代入し、両辺に共通項として残る$\boldsymbol{E}$を消去すると、 \begin{eqnarray} \boldsymbol{k}^2=\cfrac{\omega^2}{c^2} \end{eqnarray} と、平面波の分散式(dispersion relation)が得られる。
式(\ref{eq:wrotE})左辺は、円筒座標系では、 \begin{eqnarray} \nabla^2 \boldsymbol{E} = \cfrac{1}{r} \cfrac{\partial}{\partial r} \left( r \cfrac{\partial \boldsymbol{E}}{\partial r} \right) + \cfrac{1}{r^2} \cfrac{\partial^2 \boldsymbol{E}}{\partial \theta^2} + \cfrac{\partial^2 \boldsymbol{E}}{\partial z^2} \end{eqnarray} となる。従って、式(\ref{eq:wrotE})は、円柱座標系では、 \begin{eqnarray} 0 = \cfrac{1}{r} \cfrac{\partial}{\partial r} \left( r \cfrac{\partial \boldsymbol{E}}{\partial r} \right) + \cfrac{1}{r^2} \cfrac{\partial^2 \boldsymbol{E}}{\partial \theta^2} + \cfrac{\partial^2 \boldsymbol{E}}{\partial z^2} - \cfrac{\omega^2}{c^2} \boldsymbol{E} \end{eqnarray} となる。
また、磁場$\boldsymbol{B}$に関しても、全く同様の展開となる。
円筒導波管モード
平面波の回転積分に、円筒導波管を境界条件として与えると、円筒導波管の伝搬モードであるTMモードとTEモードが求まる。まず、 平面波の伝搬方向を$x-z$方向とする静止直交座標系$(x, y, z)^\flat$を定義する。この静止直交座標系では、波数ベクトルは$\boldsymbol{k}=(k_x , 0, k_z)$となる。
この静止直交座標系において、位置$\boldsymbol{r}$が、座標中心からの距離$r$、x軸からの回転角$\phi$、高さ$z$にあるとすと、
\begin{eqnarray} \boldsymbol{r}=(x,y,z)=(\sqrt{r^2-z^2} \cos \phi , \sqrt{r^2-z^2} \sin \phi, z) \end{eqnarray} となる。この静止座標系上の平面波の電場成分$\boldsymbol{E}^\flat$を回転積分$\int^{2\pi}_0d\phi$する。$k_y = 0$なので、 \begin{eqnarray} E_z&=&\int^{2\pi}_0 d\phi \boldsymbol{E}^\flat \cdot \boldsymbol{e}_z \exp \left\{ i (\omega t - k_x r \cos \phi) \right\} \nonumber \\ &=&2\pi E^\flat_z(t) J_m(k_r r) \\ \end{eqnarray} となる。ここで、$\boldsymbol{e}_z$は$z$方向の単位ベクトルである。 回転積分円筒座標系$(r, \theta, z)$で、残りの電場成分は、 \begin{eqnarray} E_r&=&2\pi E^\flat_x J'_{m}(k_r r) \\ E_\theta&=&2\pi E^\flat_y J'_{m}(k_r r) \end{eqnarray} となる。尚、回転積分円筒座標系において、$r=x$である。
円筒導波管TMモード(Transverse magnetic mode)
半径$a$の円筒導波管の管壁を完全導体と仮定する。管壁上での電界は$0$となる。これに加え、磁場ベクトルが垂直面にしか無い、恒等的に$B_z=0$となる場合を、TMモードと呼ぶ。 従って、TMモードの境界条件は、 \begin{eqnarray} E_r(a) &=& 2\pi E^\flat_x J'_{m}(k_r a)=0 \\ E_\theta(a) &=& 2\pi E^\flat_y J'_{m}(k_r a)=0 \end{eqnarray} である。従って、Maxwell方程式は、以下のように整理される。 \begin{eqnarray} \left\{ \matrix{\nabla \cdot \boldsymbol{E} = \cfrac{1}{r} \cfrac{\partial }{\partial r} (rE_r)+\cfrac{1}{r} \cfrac{\partial E_\theta}{\partial \theta} +\cfrac{\partial E_z}{\partial z}=\left. \cfrac{\rho}{\epsilon_0} \right|_{\rho=0}\cr \nabla \times \boldsymbol{E}= \left[ \matrix{ \cfrac{1}{r} \cfrac{\partial E_z}{\partial \theta} - \cfrac{\partial E_\theta}{\partial z}\cr \cfrac{\partial E_r}{\partial z} - \cfrac{\partial E_z}{\partial r}\cr \cfrac{1}{r} \cfrac{\partial}{\partial r} (r E_\theta) - \cfrac{1}{r} \cfrac{\partial E_r}{\partial \theta} } \right] = \left[\matrix{ -i\omega B_r \cr -i\omega B_\theta \cr -i\omega B_z }\right] \cr \nabla \cdot \boldsymbol{B} = \cfrac{1}{r} \cfrac{\partial }{\partial r} (rB_r)+\cfrac{1}{r} \cfrac{\partial B_\theta}{\partial \theta} +\cfrac{\partial B_z}{\partial z}=0 \cr \nabla \times \boldsymbol{B} = \left[ \matrix{ \cfrac{1}{r} \cfrac{\partial B_z}{\partial \theta} - \cfrac{\partial B_\theta}{\partial z}\cr \cfrac{\partial B_r}{\partial z} - \cfrac{\partial B_z}{\partial r}\cr \cfrac{1}{r} \cfrac{\partial}{\partial r} (r B_\theta) - \cfrac{1}{r} \cfrac{\partial B_r}{\partial \theta} } \right] = \left[\matrix{ \cfrac{i \omega}{c^2} E_r \cr \cfrac{i \omega}{c^2} E_\theta \cr \cfrac{i \omega}{c^2} E_z }\right] } \right. \nonumber \\ \rightarrow \left\{ \matrix{\nabla \cdot \boldsymbol{E} = \cfrac{1}{r} \cfrac{\partial}{\partial r} (rE_r)+\cfrac{1}{r} \cfrac{\partial E_\theta}{\partial \theta} -ik_z E_z=0 \cr \nabla \times \boldsymbol{E}= \left[ \matrix{ \cfrac{1}{r} \cfrac{\partial E_z}{\partial \theta} + ik_z E_\theta \cr -ik_z E_r - \cfrac{\partial E_z}{\partial r}\cr \cfrac{1}{r} \cfrac{\partial}{\partial r} (r E_\theta) - \cfrac{1}{r} \cfrac{\partial E_r}{\partial \theta} } \right] = \left[\matrix{ -i\omega B_r \cr -i\omega B_\theta \cr 0 }\right] \cr \nabla \cdot \boldsymbol{B} = \cfrac{1}{r} \cfrac{\partial }{\partial r} (rB_r)+\cfrac{1}{r} \cfrac{\partial B_\theta}{\partial \theta} =0 \cr \nabla \times \boldsymbol{B} = \left[ \matrix{ ik_z B_\theta \cr -ik_z B_r \cr \cfrac{1}{r} \cfrac{\partial}{\partial r} (r B_\theta) - \cfrac{1}{r} \cfrac{\partial B_r}{\partial \theta} } \right] = \left[\matrix{ \cfrac{i \omega}{c^2} E_r \cr \cfrac{i \omega}{c^2} E_\theta \cr \cfrac{i \omega}{c^2} E_z }\right] } \right. \end{eqnarray} Bessel関数の公式$J'_{m}=mJ_{m+1}$となる。$J_m(k_n a)=0$となる$k_n a$は、振動関数である第一種Bessel関数が$0$となる値であり、以下の数表に示す飛び飛びの値となる。
| m-n | 1 | 2 | 3 | 4 |
| 0 | 3.832 | 7.016 | 10.173 | 13.324 |
| 1 | 1.841 | 5.331 | 8.536 | 11.706 |
| 2 | 3.054 | 6.706 | 9.969 | 13.170 |
| 3 | 4.201 | 8.015 | 11.346 | 14.580 |
TMモードの導波管軸方向の電界$E_z$は、$k_r \equiv k_{mn}\equiv constant$と置き換え、 \begin{eqnarray} E_z &=& E_0 \exp(i \omega t) J_m(k_{mn} r) \cos(m \theta) \cos(k_z z) \\ k_z &=& \sqrt{(\cfrac{\omega^2}{c^2}- k^2_{mn})} \label{eq:TMcuttoff} \end{eqnarray} となる。 この時の電界$E_\theta$は、 \ref{eq:rotE} E_\theta &=& E_0 \exp(i \omega t) J_m(k_r r) \cos(m \theta) \cos(k_z z) \\ 式(\ref{eq:TMcuttoff})は、$k_z=0$の時、その導波管が伝え得る最低周波数である遮断周波数(cut off frequency):$f=\omega/2\pi =ck_{01}/2\pi$を与える。
円筒導波管TEモード(Transverse electric mode)
\begin{eqnarray} H_z &=& H_0 J_m(k_r r) \cos(m \phi) \cos(k_z z) \\ k_r &=& k'_{mn}/a \\ \omega^2 &=& c^2 (k_p^2+k_z^2) \\ k_z &=& (\omega^2-c^2 k_p^2)^{1/2} \end{eqnarray} 位相因子を残すと \begin{eqnarray} H_z &=& H_0 \exp{i(\omega t- m \phi- k_z z)} J_m(k_p r) \\ H_r &=& (H_0^2-H_r^2)^{1/2} \end{eqnarray} \begin{eqnarray} D^{(E\pm)} &=& \left[ 1+(p-q) \cfrac{k_\bot k_0}{} \right] \nonumber \\ D^{(B\pm)} &=& \nonumber \\ Q_n &=& J_m (x_{\bot n} R_b) N'_m (x_{\bot n} R_b) - J'_m (x_{\bot n} R_b) N_m (x_{\bot n} R_b) \end{eqnarray} \begin{eqnarray} k_{\parallel n} &=& k_z + n k_0 \label{eq:defkparan} \\ k^2_{\bot n} &=& \cfrac{\omega^2}{c^2}-k^2_{\parallel n} \label{eq:defkbotn} \end{eqnarray} 円筒波型導波管の境界条件、 \begin{eqnarray} 0 &=& E_{t}(r=R_W) \propto E_z + E_t \cfrac{{\rm{d}} R_W}{{\rm{d}}z} \\ 0 &=& E_{\theta}(r=R_W) \end{eqnarray} は、Floquetの定理より、 \begin{eqnarray} 0 &=& \sum^{\infty}_{n=-\infty} \exp ik_n z \left({1+\cfrac{ik_n}{\cfrac{\omega^2}{c^2} - k^2_n} \cfrac{{\rm{d}} R_W}{{\rm{d}}z} } \right) \left[D_n J_m (k_{\bot n} R_W) + E_n N_m (k_{\bot n} R_W) \right] \\ 0 &=& \sum^{\infty}_{n=-\infty} \exp ik_n z \cfrac{\cfrac{\omega}{c} }{ \cfrac{\omega^2}{c^2} - k^2_n } \cfrac{{\rm{d}} R_W}{{\rm{d}}r} \left[D_n J_m (k_{\bot n} R_W) + E_n N_m (k_{\bot n} R_W) \right] \end{eqnarray} よって、 \begin{eqnarray} \left[ \matrix{ D^{(E+)} (\omega, k_{n}) & D^{(E-)}(\omega, k_{n}) \cr D^{(B+)}(\omega, k_{n}) & D^{(B-)}(\omega, k_{n}) } \right] \cdot \left[\matrix{A^{(+)} \cr A^{(-)} }\right] =0 \end{eqnarray} となる。 \begin{eqnarray} D^{(E \pm)}_{\alpha n} (\omega, k_{n}) &=& \left[ 1+\left( n - \alpha \right) \cfrac{k_n k_0}{k_{\bot n}} \right] \left( C^{(J)}_{\alpha n} K^{(1\pm)}_n + C^{(N)}_{\alpha n} K^{(2\pm)}_n \right) -i \cfrac{m \omega}{c k^2_{\bot n}} \left( C^{(J'_m)}_{\alpha n} K^{(3\pm)}_n + C^{(N'_m)}_{\alpha n} K^{(4\pm)}_n \right) \\ D^{(B \pm)}_{\alpha n} (\omega, k_{n}) &=& \cfrac{\omega}{c k_{\bot n}} \left( C^{(J')}_{\alpha n} K^{(1\pm)}_n + C^{(N')}_{\alpha n} K^{(2\pm)}_n \right) - \cfrac{m k_n}{c k^2_{\bot n}} \left( C^{(J_m)}_{\alpha n} K^{(3\pm)}_n + C^{(N_m)}_{\alpha n} K^{(4\pm)}_n \right) \end{eqnarray} ここで、 \begin{eqnarray} C^{(J)}_{\alpha n} &=& \int^{\pi/k_0}_{-\pi/k_0} {\rm{d}}z J_m (k_{\bot n} R_W) \exp [i(n-\alpha) k_0 z] \nonumber \\ C^{(N)}_{\alpha n} &=& \int^{\pi/k_0}_{-\pi/k_0} {\rm{d}}z N_m (k_{\bot n} R_W) \exp [i(n-\alpha) k_0 z] \nonumber \\ C^{(J'_m)}_{\alpha n} &=& \int^{\pi/k_0}_{-\pi/k_0} {\rm{d}}z \cfrac{m}{R_W} \cfrac{{\rm{d}}R_W}{{\rm{d}}z} J_m (k_{\bot n} R_W) \exp [i(n-\alpha) k_0 z] \nonumber \\ C^{(N'_m)}_{\alpha n} &=& \int^{\pi/k_0}_{-\pi/k_0} {\rm{d}}z \cfrac{m}{R_W} \cfrac{{\rm{d}}R_W}{{\rm{d}}z} N_m (k_{\bot n} R_W) \exp [i(n-\alpha) k_0 z] \nonumber \\ C^{(J')}_{\alpha n} &=& \int^{\pi/k_0}_{-\pi/k_0} {\rm{d}}z J'_m (k_{\bot n} R_W) \exp [i(n-\alpha) k_0 z] \nonumber \\ C^{(N')}_{\alpha n} &=& \int^{\pi/k_0}_{-\pi/k_0} {\rm{d}}z N'_m (k_{\bot n} R_W) \exp [i(n-\alpha) k_0 z] \nonumber \\ C^{(J_m)}_{\alpha n} &=& \int^{\pi/k_0}_{-\pi/k_0} {\rm{d}}z \cfrac{m}{R_W} J_m (k_{\bot n} R_W) \exp [i(n-\alpha) k_0 z] \nonumber \\ C^{(N_m)}_{\alpha n} &=& \int^{\pi/k_0}_{-\pi/k_0} {\rm{d}}z \cfrac{m}{R_W} N_m (k_{\bot n} R_W) \exp [i(n-\alpha) k_0 z] \nonumber \\ K^{(1 +)}_{n} &=& \cfrac{1}{Q_n} \left[ J_m (k_{\angle n} R_b) N'_m (k_{\bot n} R_b) - \cfrac{k_{\bot n}}{k_{\angle n}} \left( 1- \cfrac{\omega^2_b}{\gamma^3_0 \omega'^2} \right) J'_m (k_{\angle n} R_b) N_m (k_{\bot n} R_b) \right] \nonumber \\ K^{(2 +)}_{n} &=& - \cfrac{1}{Q_n} \left[ J_m (k_{\angle n} R_b) J'_m (k_{\bot n} R_b) - \cfrac{k_{\bot n}}{k_{\angle n}} \left( 1- \cfrac{\omega^2_b}{\gamma^3_0 \omega'^2} \right) J'_m (k_{\angle n} R_b) J_m (k_{\bot n} R_b) \right] \nonumber \\ K^{(1 -)}_{n} = K^{(3 +)}_{n} &=& \cfrac{1}{Q_n} \cfrac{m}{R_b} \cfrac{ \omega^2_b}{\gamma_0 k_{\bot n} } \cfrac{\left( k_n - \cfrac{\omega v_0}{c^2} \right)}{c\omega' k^2_{\angle n}} J_m (k_{\angle n} R_b) N_m (k_{\bot n} R_b) \nonumber \\ K^{(2 -)}_{n} = K^{(4 +)}_{n} &=& - \cfrac{1}{Q_n} \cfrac{m}{R_b} \cfrac{ \omega^2_b}{\gamma_0 k_{\bot n} } \cfrac{\left( k_n - \cfrac{\omega v_0}{c^2} \right)}{c\omega' k^2_{\angle n}} J_m (k_{\angle n} R_b) J_m (k_{\bot n} R_b) \nonumber \\ K^{(3 -)}_{n} &=& \cfrac{1}{Q_n} \left[ J_m (k_{\angle n} R_b) N'_m (k_{\bot n} R_b) - \cfrac{k_{\bot n}}{k_{\angle n}} J'_m (k_{\angle n} R_b) N_m (k_{\bot n} R_b) \right] \nonumber \\ K^{(4 -)}_{n} &=& \cfrac{1}{Q_n} \left[ J_m (k_{\angle n} R_b) J'_m (k_{\bot n} R_b) - \cfrac{k_{\bot n}}{k_{\angle n}} J'_m (k_{\angle n} R_b) J_m (k_{\bot n} R_b) \right] \end{eqnarray} ここで、$Q_n$は、 \begin{eqnarray} Q_n &=& J_m (k_{\bot n} R_b) N'_m (k_{\bot n} R_b) - J'_m (k_{\bot n} R_b) N_m (k_{\bot n} R_b) \end{eqnarray} である。従って分散式は、 \begin{eqnarray} 0={\rm{det}} \left| \matrix{ D^{(E+)} (\omega, k_{n}) & D^{(E-)}(\omega, k_{n}) \cr D^{(B+)}(\omega, k_{n}) & D^{(B-)}(\omega, k_{n}) } \right| \end{eqnarray} となる。